Biot-Savart Law¶

The Biot-Savart Law derives the magnetic field B due to a current:

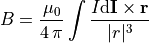
$B = \frac{\mu_0}{4 \, \pi} \int \frac{I \textrm{d}\vec{I} \times \vec{r}}{|r|^3}$

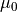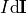Here, $\mu_0$ is the magnetic constant, $\textrm{d}\vec{I}$ is the infinitesimal length and direction of a section of infinitesimally thin wire current we are integrating over, I is the amount of current in that section, and r is the displacement vector from the section of wire current to the point where B is measured. $I \textrm{d}\vec{I}$ may also be replaced with 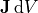$\vec{J} \, \textrm{d}V$ if a current density J occupies a volume element dV.

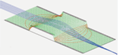
SIMION Specific¶

SIMION 8.0.3 can compute magnetic fields from wire currents using the Biot-Savart law using the simionx.MField - Biot-Savart magetic field calculations library. In SIMION 8.1.0.19, these wires can also be drawn on the SIMION View screen. Examples of this include

SIMION Example: solenoid (see also Solenoid Magentic Field)
SIMION Example: helmholtz_coil (see also Helmholtz Coil)

See also Magnets and Wikipedia: Biot-Savart_law.

A thick wire can be approximated with many thin wires. See Example(helmholtz_coil) (thick_coil sub-example) added 2018-03-08.


[Optional] Your name:	email:	phone: