Emittance¶

Overview¶

Beam emittance provides a measure of the quality of a beam, particularly the laminarity of the beam. Beam emittance is a parameter equal or related to the volume (or area) occupied by a particle beam when represented in a phase space consisting of position and momentum. In phase space, each particle in the beam is represented by a six-dimensional vector $(x,y,z,p_x,p_y,p_z)$ consisting of the x, y, and z components of its position and momentum vectors. Although this phase space is in general six-dimensional, if the motions in the x, y, and z directions are independent, we can treat them separately. The emittance in the x direction is related to the area of a 2D plot of $p_x$ v.s. $x$ , and likewise for the y and z directions. Often only the two directions transverse to the beam are of interest, and the longitudinal direction (conventionally z) is ignored.

Criteria for zero emittance: Zero emittance can occur if there is zero area in phase space, such as if there is no spread in either position or momentum or if there are spreads in both position and momentum but these two values are perfectly correlated (e.g. the phase space plot is a diagonal line with zero area). A perfectly laminar beam converging to a point exhibits this. A curved line in phase space, which has zero area but does not demonstrate perfect linear correlation, may or may not be characterized with zero emittance depending on how we define emittance.

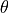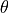Alternatives to momentum: In computing emittance, the momentum, e.g. $p_x$ , may be replaced with $x' = dx/dz = (dx/dt)/(dz/dt) = v_x/v_z$ . This (x,x’) is called trace space. This slope x’ may also be thought of as an angle $\theta$ with units in radians since $dx/dz = tan(\theta) \approx \theta$ at small $\theta$ (paraxial approximation).

Definitions of emittance: There are many possible definitions for emittance depending on how we represent “area”. A fractional emittance, such as the 90% fractional emittance $\epsilon_{90}$ , is the volume occupied by regions of the beam whose intensity exceeds some threshold such that this volume contains 90% of the particles. One statistical definition of area is the root-mean-square emittance, $\epsilon_{rms,x}$ , defined as

$\epsilon_{rms,x} = \sqrt{ \langle xx \rangle \langle x'x' \rangle - \langle xx' \rangle^2 }$

It’s equivalently $\epsilon_{rms,x} = \langle xx \rangle \langle x'x' \rangle \sqrt{1 - r^2}$ , where r is the correlation coefficient between x and x’, so the RMS definition depends not only on the area of the box $\langle xx \cdot \rangle \langle x'x' \rangle$ but also the linearity of the dependence (r). RMS emittance may also be thought of as a statistical mean area [2].

The emittance may be defined as

$\epsilon_x = 4 \epsilon_{rms,x}$

One motivation for this is that in the special case of a uniform axis-aligned ellipse in trace space, $\epsilon_x$ corresponds to the product of the major and minor radii, and the area of this ellipse is $\pi \epsilon_x$ .

The beam ellipse can be expressed in terms of so-called Twiss (or Courant-Snyder) parameters based on the second moments used in the RMS emittance:

$\gamma x^2 + 2 \alpha x x' + \beta x'^2 = \epsilon_{rms}$

$\alpha = -\frac{\langle xx' \rangle}{\epsilon_{rms}}, \beta = \frac{\langle xx \rangle}{\epsilon_{rms}}, \gamma = \frac{\langle x'x' \rangle}{\epsilon_{rms}}, \beta \gamma - \alpha^2 = 1$

Units on emittance include rad*m and mm*mrad, sometimes multiplied by the factor $\pi$ . The units may be specified as “pi*mm*mrad” to clarify that the $\pi$ has not been absorbed into the number.[3]

Normalized emittance (as opposed to geometric emittance based on a fraction of area or volume) is $\epsilon_n = \beta \gamma \epsilon$ , where $\beta = \overline{v} / c$ and $\gamma = 1/\sqrt{1 - \beta^2}$ are the relativistic parameters, c is the velocity of light, and $\overline{v}$ is the velocity (or averaged velocity). The advantage of normalized emittance is that under certain conditions it is constant under beam acceleration (see Wikipedia:Liouville’s_theorem_(Hamiltonian) and more specifically [1,2]).

Computing Emittance in SIMION¶

There’s more than one way to go about computing emittance in SIMION. At the most basic level, all that is required are the position and velocity vectors of all particles when crossing some plane, for you can then apply the above formulas. You can either apply the formulas yourself outside of SIMION (e.g. in Excel) or do this calculation entirely inside SIMION (can be more convenient).

SIMION’s Data Recording functions (available in all versions of SIMION, including 7.0-8.0) can extract the required data. Just enable recording of x, y, z, vx, vy, and vz parameters when “x=” some value (under “what data to record” and “when to record”). Preferably set the format to “Delimited” for easier input into programs like Excel and set it to output to a file. Exporting “data recording” results to text file has more information on exporting.

Alternately, you may use a SIMION user program to measure this data and compute emittance. This is convenient because emittance will be computed (and optionally phase plots plotted) automatically each time you Fly’m. See SIMION Example: emittance, SIMION Example: test_plane, and SIMION Example: excel (phase plot) for some examples of these capabilities.

Defining a Beam with a Given Emittance¶

If you’d like to define a beam with a given value of emittance, note that emittance doesn’t uniquely define the beam. Emittance can be roughly thought of as an area (or hypervolume), and there is an infinite number of shapes with a given area. However, perhaps imposing further constraints such as on the general shape of the beam could allow emittance to uniquely define the beam. You can of course define a beam, measure its emittance, and adjust the beam definition as necessary to obtain the emittance you want.


[Optional] Your name:	email:	phone:

Emittance¶

Overview¶

Computing Emittance in SIMION¶

Defining a Beam with a Given Emittance¶

See Also¶