Laplace Equation¶
In electrostatics, the Laplace equation can calculate the potentials throughout some volume of empty space given certain known conditions on the boundary surface enclosing that volume. Those boundary conditions are typically voltages on the surfaces of electrodes (see Dirichlet Boundary Conditions) but can also be planes of mirror symmetry (see Neumann Boundary Condition).
The Laplace equation is

for electric field,  . It is simply a statement that the
divergence of electric field is zero everywhere.
It can also be written in terms of potential,
. It is simply a statement that the
divergence of electric field is zero everywhere.
It can also be written in terms of potential, 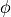 (since
(since
 ):
):

The Laplace equation is a special case of the Poisson Equation in which zero space-charge is assumed throughout the volume (not including the boundary surface, which is typically made up of electrode surfaces having surface charges).
SIMION Specific Notes¶
SIMION’s “Refine” function solves the Laplace equation in a Potential Array. Electrode points in the PA are taken as Dirichlet boundary conditions with the given potential, and non-electrode PA edges are taken as Neumann boundary conditions (in most conditions–see Neumann Boundary Condition).
