Collision Model HS1

This SIMION user program implements a rather complete hard-sphere collision model. Collision models are useful for simulating non-vacuum conditions, in which case ions collide against a background gas and are deflected randomly.

Features and assumptions of the model:

  • Ion collisions follow the hard-sphere collision model. Energy transfers occur solely via these collisions.

  • Ion collisions are elastic.

  • Background gas is assumed neutral in charge.

  • Background gas velocity follows the Maxwell-Boltzmann distribution.

  • Background gas mean velocity may be non-zero.

  • Kinetically cooling and heating collisions are simulated.

  • Background gas as a whole is unaffected by ion collisions.

Code

  • SIMION 8 includes a Lua version (collision_hs1 example). It is more updated and documented than earlier PRG/SL versions.

Evaluation and Comparison

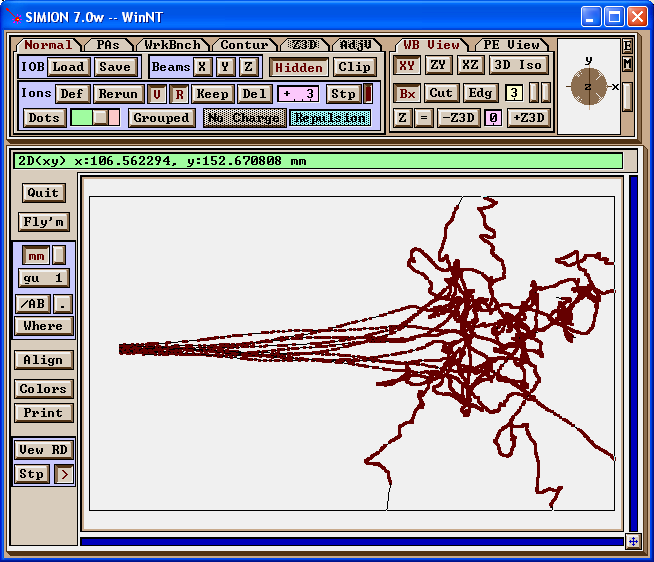
The figure below shows ion trajectories in the HS1 collision model (dots mark collision events). Conditions: ions of mass 200 amu, 15 angstrom collision diameter, and initial velocity to the right at 24 eV colliding against a He background gas with 2 angstrom collision diameter, 4 mTorr pressure, and 275 K temperature. Collisions tend to kinetically cool ions initially. As ions slow down, mean-free-path decreases and the scattering effect increases.

_images/collision_hs1_slow.png

The below figures area plots of ion speed per collision number using the HS1 collision model as well as the earlier dahl_drag.prg and _Trap/INJECT.PRG in SIMION 7.0 models for comparison. The Ling1997 paper (Figure 4) provides a similar graph for its collision model under the same conditions. The HS1 and dahl_drag.prg models are in fairly good agreement in this aspect. However, these differ from the Ling1997 and _Trap/INJECT.PRG graphs, which are similar to each other and show almost twice as rapid dampening. (Note: full details of Ling1997 are not available.) The reduced dampening in the former models seems partly due to the inclusion of heating collisions from behind the ions.

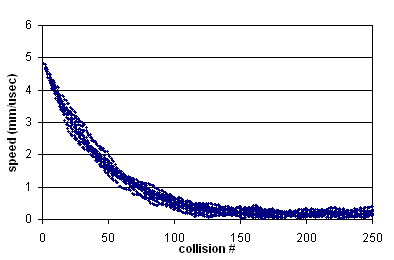
_images/collision_hs1_graph2.png

Fig. 63 Figure: Dampening using Collision Model HS1

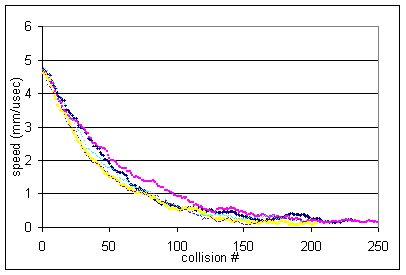
_images/collision_hs1_graph1.png

Fig. 64 Figure: Dampening using Collision Model dahl_drag.prg

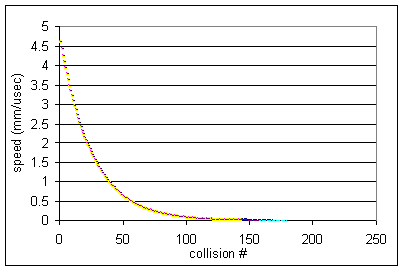
_images/collision_hs1_graph3.png

Fig. 65 Figure: Dampening using Collision Model _Trap/INJECT.PRG in SIMION 7.0 (also resembles Ling1997)

Despite these similarities in the above regard, the models can still be quite different. For example, HS1 model supports a variable mean-free-path (unlike dahl_drag.prg), and this affects the frequency of collisions, especially as speeds change. Models can also handle angular scattering differently (e.g. _Trap/INJECT.PRG does not provide any angular scattering).

Appendix: Derivation of Mean Relative Speed

This program calculates mean relative speed between the ion and background gas in order to calculate mean-free-path. The following is a derivation of the equation for mean relative velocity.

Compute average relative speed c of a single particle (ion) against a background gas (gas). The background gas is assumed to be Maxwell distributed in velocity.

We start with

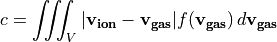
c = \iiint_V |\mathbf{v_{ion}} - \mathbf{v_{gas}}| f(\mathbf{v_{gas}}) \, d\mathbf{v_{gas}}

where f is the three-dimensional Maxwell distribution given by

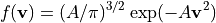
f(\mathbf{v}) = (A/\pi)^{3/2} \exp(-A\mathbf{v}^2)

such that 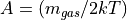A = (m_{gas} / 2 k T).

Substituting,

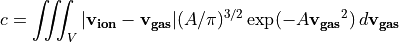
c = \iiint_V |\mathbf{v_{ion}} - \mathbf{v_{gas}}| (A/\pi)^{3/2} \exp(-A\mathbf{v_{gas}}^2) \, d\mathbf{v_{gas}}

Let 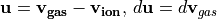\mathbf{u} = \mathbf{v_{gas}} - \mathbf{v_{ion}}, \, d\mathbf{u} = d\mathbf{v}_{gas}.

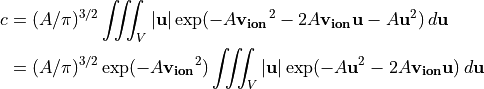
\begin{align*} c & = (A / \pi)^{3/2} \iiint_V |\mathbf{u}| \exp(-A\mathbf{v_{ion}}^2 - 2A\mathbf{v_{ion}}\mathbf{u} - A\mathbf{u}^2) \, d\mathbf{u} \\ & = (A/\pi)^{3/2} \exp(-A\mathbf{v_{ion}}^2) \iiint_V |\mathbf{u}| \exp(-A\mathbf{u}^2 - 2A\mathbf{v_{ion}}\mathbf{u}) \, d\mathbf{u} \end{align*}

Convert to spherical coordinates and let r = |\mathbf{u}|, a = |\mathbf{v_{ion}}|, \mathbf{v_{ion}} \cdot \mathbf{u} = |\mathbf{v_{ion}}||\mathbf{u}|\cos \theta.

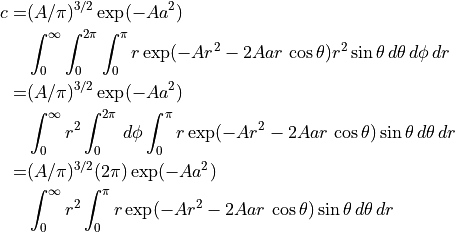
\begin{align*} c = & (A/\pi)^{3/2} \exp(-Aa^2) \\ & \int_0^{\infty} \int_0^{2\pi} \int_0^{\pi} r \exp(-Ar^2 - 2Aar \, \cos \theta) r^{2} \sin \theta \, d\theta \, d\phi \, dr \\ = & (A/\pi)^{3/2} \exp(-Aa^2) \\ & \int_0^{\infty} r^{2} \int_0^{2\pi} \, d\phi \int_0^{\pi} r \exp(-Ar^2 - 2Aar \, \cos \theta) \sin \theta \, d\theta \, dr \\ = & (A/\pi)^{3/2} (2\pi) \exp(-Aa^2) \\ & \int_0^{\infty} r^{2} \int_0^{\pi} r \exp(-Ar^{2} - 2Aar \, \cos \theta) \sin \theta \, d\theta \, dr \end{align*}

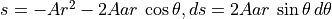Let s = -Ar^2 - 2Aar \, \cos\theta, ds = 2Aar \, \sin \theta \, d\theta.

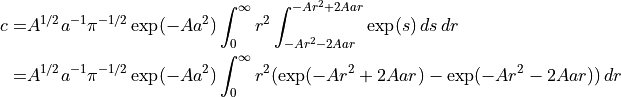
\begin{align*} c = & A^{1/2} a^{-1} \pi^{-1/2} \exp(-Aa^2) \int_0^{\infty} r^{2} \int_{-Ar^2 - 2Aar}^{-Ar^2 + 2Aar} \exp(s) \, ds \, dr \\ = & A^{1/2} a^{-1} \pi^{-1/2} \exp(-Aa^2) \int_0^{\infty} r^{2} (\exp(-Ar^2 + 2Aar) - \exp(-Ar^2 - 2Aar)) \, dr \end{align*}

To solve this integral, we use

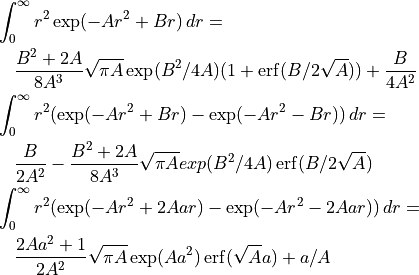
\begin{align*} & \int_0^{\infty} r^{2} \exp(-Ar^2 + Br) \, dr = \\ & \quad \frac{B^2+2A}{8A^3} \sqrt{\pi A} \exp(B^2/4A) (1 + \operatorname{erf}(B/2\sqrt{A})) + \frac{B}{4A^2} \\ & \int_0^{\infty} r^{2} (\exp(-Ar^2 + Br) - \exp(-Ar^2 - Br)) \, dr = \\ & \quad \frac{B}{2A^2} - \frac{B^2+2A}{8A^3} \sqrt{\pi A} exp(B^2/4A) \operatorname{erf}(B/2\sqrt{A}) \\ & \int_0^{\infty} r^{2} (\exp(-Ar^2 + 2Aar) - \exp(-Ar^2 - 2Aar)) \, dr = \\ & \quad \frac{2Aa^2+1}{2A^2} \sqrt{\pi A} \exp(Aa^2) \operatorname{erf}(\sqrt{A}a) + a/A \end{align*}

Substituting,

\begin{align*} c = & A^{1/2} \pi^{-1/2} a^{-1} \exp(-Aa^2) \\ & (\frac{2Aa^2 + 1}{2A^2}\pi^{1/2} \exp(Aa^2)A^{1/2}\operatorname{erf}(A^{1/2}a) + (a/A)) \\ & (2A^{-1/2} \pi^{-1/2}) \cdot \left[ \frac{\pi^{1/2}}{2} (A^{1/2}a + \frac{1}{2} A^{-1/2}a^{-1}) \operatorname{erf}(A^{1/2}a) + \frac{1}{2}\exp(-Aa^2) \right] \end{align*}

Let

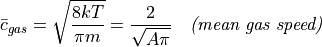
\bar{c}_{gas} = \sqrt{\frac{8kT}{\pi m}} = \frac{2}{\sqrt{A\pi}} \quad \textit{(mean gas speed)}

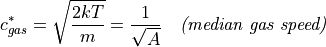
c^{*}_{gas} = \sqrt{\frac{2kT}{m}} = \frac{1}{\sqrt{A}} \quad \textit{(median gas speed)}

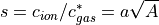
s = c_{ion}/c^{*}_{gas} = a\sqrt{A}

Substituting gives the result:

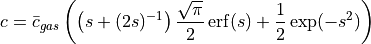
c = \bar{c}_{gas} \left(\left(s + (2s)^{-1}\right)\frac{\sqrt{\pi}}{2}\operatorname{erf}(s) + \frac{1}{2}\exp(-s^2)\right)

This result is in agreement with Ding2002.

Note the following resuts:

As c_{ion} \rightarrow 0, c \rightarrow \bar{c}_{gas}.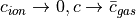

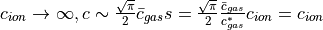Also, as c_{ion} \rightarrow \infty, c \sim \frac{\sqrt{\pi}}{2} \bar{c}_{gas} s = \frac{\sqrt{\pi}}{2} \frac{\bar{c}_{gas}}{c^{*}_{gas}} c_{ion} = c_{ion}.

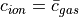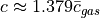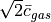Further, if c_{ion} = \bar{c}_{gas}, then c \approx 1.379 \bar{c}_{gas}, which is approximately the average relative speed between the gas particles themselves (\sqrt{2}\bar{c}_{gas}).

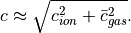The above results provide a rough justification for the approximation c \approx \sqrt{c_{ion}^2 + \bar{c}_{gas}^2}. .