Stefan-Boltzmann Law¶

The Stefan-Boltzmann Law relates temperature (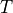 $T$ ) to radiated thermal energy (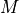 $M$ ) for a blackbody object.[1]

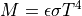
$M = \epsilon \sigma T^4$

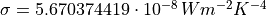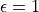where $\sigma = 5.670374419 \cdot 10^{-8} \, W m^{-2} K^{-4}$ (CODATA2022) and $\epsilon = 1$ for an ideal radiator, as described in [1].

When the temperature of the surroundings (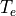 $T_e$ ) is nonegligible [2],

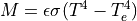
$M = \epsilon \sigma (T^4 - T_e^4)$

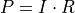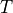If the electrical power $P = I \cdot R$ input into a thermionic filament is largely dissipated as radiation and as a black body, then temperature $T$ of the filament could be estimated from input current 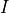$I$ by way of Stefan-Boltzmann Law.


[Optional] Your name:	email:	phone:

Stefan-Boltzmann Law¶

See Also¶