Lorentz Force Law

The Lorentz force law describes the force on a point of charge q in an electric (E) and/or magnetic (B) field:

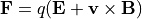
\vec{F} = q (\vec{E} + \vec{v} \times \vec{B})

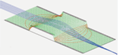
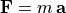The trajectory of a point charge through an electromagnetic field can be determined using this equation along with Newton’s second law (\vec{F} = m \, \vec{a}).

Typically, for trajectory calculations, particles like electrons and ions are treated as point charges, although in practice particles could have rotational, vibrational, or internal energies, and dipoles in the particles could even experience different fields (e.g. like Wikipedia: Dielectrophoresis).

SIMION Specific

By default, particle motion in SIMION is governed by the Lorentz force law. However, you can use SIMION’s scripting language to modify or replace this equation with whatever you want. This includes adding the force of gravity, applying a viscous drag force according to the Mobility Equation, adding diffusion or ion-gas collision model effects, etc.

Gravity

Here’s an illustrative example of a workbench user program that adds the force (actually acceleration) of gravity to a particle. This acceleration is added to the acceleration of the electric and/or magnetic field already calculated by SIMION (from the Lorentz force law):

simion.workbench_program()

-- Add gravity acceleration to acceleration vector.
-- Note: this g is approximate and varies over
-- location, http://en.wikipedia.org/wiki/Gravity_of_Earth .
function segment.accel_adjust()
  local g = -9.81E-9   -- Acceleration of gravity, mm/usec^2.
  ion_ay_mm = ion_ay_mm + g
end

For most cases, gravity is negligible, unless particles have very low velocity, as may occur for very massive particles. A proton accelerated by 100 V would have a velocity of about 138 mm/usec, which would be affected little by the value of g along a distance of 138 mm or so. Such masses, voltages, and distances are typical of many benchtop-sized particle optics systems.

Acceleration

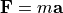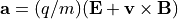The acceleration observed by a particle according to the Lorentz force law depends on the charge/mass ratio (q/m) of the particles and not on the individual values of mass and charge. This is seen by combing the Lorentz force law with \v{F} = m \v{a} to obtain \v{a} = (q/m) (\v{E} + \vec{v} \times \vec{B}).

In fact, you could even enter arbitrary mass and charge values into SIMION, as long as the ratio of charge/mass matches your actual particles and you define/interpret particle KE in terms of the mass entered since 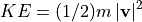KE = (1/2) m \left|\v{v}\right|^2 (or just use velocity rather than KE). Prior to SIMION 8.1.1.31 (which increased mass, charge, and KE limits), a particle with mass greater than 1E+9 u was not easily entered, but the above trick allowed overcomming it. Another option was to define an accel_adjust segment in a user program that rescales the acceleration vector computed by SIMION as appropriate. Just for illustration, to rescale SIMION’s computed acceleration by a factor of 10:

simion.workbenc_program()
function segment.accel_adjust()
  local scale = 10
  ion_ax_mm = ion_ax_mm * scale
  ion_ay_mm = ion_ay_mm * scale
  ion_az_mm = ion_az_mm * scale
end