Mobility Equation¶
The mobility equation describes the drift (terminal) speed (vt) of a particle throuh some medium (e.g. high pressure gas) in the presence of an electric field (E) with magnitude E:
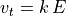
The constant of proportionality k is called the mobility constant and is specific to the type of the particle, such as its collision cross section, and the type of the medium (such as gas chemical composition, pressure and temperature).
The fact that different particles have different mobility constants is used to good effect in ion mobility spectrometry (IMS) to separate ions.
Although k depends on gas pressure P and temperature T, these effects can be removed by re-expressing k as a reduced mobility, which is the mobility at standard temperature and pressure (STP) conditions:
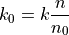
Here, n is the number density of background gas particles under current conditions (n) and standard conditions (n 0). n can be related to P and T via the ideal gas law: PV = nRT. Note, however, that the linearity between k and k0 may only be approximate within certain limits, and the ideal gas law might not hold exactly.
k is not always a constant but could depend on E. This is particularly an issue at high fields, which is used to good effect in high-field asymmetric-waveform ion mobility spectrometry (FAIMS). See the SIMION Example: faims documentation for details.
SIMION Specific¶
These SIMION examples relate to mobility:
SIMION Example: drag - Stokes’ law drag force calibrated to match mobility
SIMION Example: collision_sds - combined mobility and diffusion collision model, for high pressures
SIMION Example: collision_hs1 - hard-sphere collision model, for low pressures (free molecular), and is not a mobility model.
SIMION Example: ims - simple ion mobility example
SIMION Example: faims - FAIMS example, based on extension to the SDS model, with detailed FAIMS documentation
Other Articles¶
Travelling Wave
GilesPringle2004. Giles, Kevin. Pringle, Steven D. Worthington, Kenneth R. Little, David. Wildgoose, Jason L. Bateman, Robert H. Applications of a travelling wave-based radio-frequency-only stacked ring ion guide Rapid Communications in Mass Spectrometry. volume 18, issue 20, year 2004, pages 2401-2414 doi:10.1002/rcm.1641 “RF ion guide based on a stack of ring electrodes. Ion propulsion is produced by superimposing a voltage pulse on the confining RF of an electrode and then moving the pulse to an adjacent electrode and so on along the guide to provide a travelling voltage wave on which the ions can surf.” (highly cited)
Langridge, David. Giles, Kevin. Hotes, John B. Simulation of Ion Motion in a Travelling Wave Mobility Separator using a Hard-Sphere Collision Model 2008 poster. Waters http://www.waters.com/webassets/cms/library/docs/720002663en.pdf using SIMION HS1 collision model
Dheeraj S. Namburu, Jody C. May, John A. McLean. Experimental Validation of an Ion Simulation Model for Traveling Wave Ion Mobility Spectrometry https://www.youngscientistjournal.org/wp-content/uploads/sites/16/2015/04/Namburu.pdf
EwingZucker2013. Ewing, Michael A. Zucker, Steven M. Valentine, Stephen J. Clemmer, David E. Overtone Mobility Spectrometry: Part 5. Simulations and Analytical Expressions Describing Overtone Limits. Journal of The American Society for Mass Spectrometry. volume 24, issue 4, year 2013, pages 615-621. doi:10.1007/s13361-012-0559-8
HamidIbrahim2015. Hamid, Ahmed M. Ibrahim, Yehia M. Garimella, Sandilya V. B. Webb, Ian K. Deng, Liulin. Chen, Tsung-Chi. Anderson, Gordon A. Prost, Spencer A. Norheim, Randolph V. Tolmachev, Aleksey V. Smith, Richard D. Characterization of Traveling Wave Ion Mobility Separations in Structures for Lossless Ion Manipulations. Analytical Chemistry, volume 87, issue 22, year 2015, pages 11301-11308 doi:10.1021/acs.analchem.5b02481 https://www.osti.gov/pages/servlets/purl/1228340
Proteins in Aqueous Nanodrops: Folding, Unfolding, and Gas-Phase Conformations Measured by Mass Spectrometry. Daniel Mortensen. Dissertation, University of California, Berkeley. 2016. http://digitalassets.lib.berkeley.edu/etd/ucb/text/Mortensen_berkeley_0028E_16526.pdf
Ion Funnel
SchafferTang1997. Schaffer, Scott A. Tang, Keqi. Anderson, Gordon A. Prior, David C. Udseth, Harold R. Smith, Richard D. A novel ion funnel for focusing ions at elevated pressure using electrospray ionization mass spectrometry Rapid Communications in Mass Spectrometry, volume 11, issue 16, year 1997, pages 1813-1817 doi:10.1002/(SICI)1097-0231(19971030)11:16<1813::AID-RCM87>3.0.CO;2-D “ion funnel concept we describe is supported by results of SIMION simulations”
