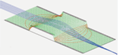
Poisson Solver in SIMION¶
Overview¶
In SIMION 8.1.0, the electromagnetic field solver (Refine function) has been extended to support solving the Poisson Equation. As before, the Refine function can calculate potentials inside a volume defined by electrodes with potentials, but the new Poisson solving capability allows it to also handle the case when a known, arbitrary distribution of Space Charge density fills that volume (such as due to high current charged particle beams or charged insulators). Dielectrics are also supported.
Applications¶
Taking into account space-charge density can be important for certain problems. Space-charge effects tends to be most severe for a slowly moving, high current beam confined in a small volume, for this causes a large space-charge density and large periods of time over which the fields from that space-charge density can have an effect on charged particle motion. A typical example is the beam near the surface of a thermionic cathode operated at maximum (space-charge-limited) current, for here the beam is not just at high current but also at low energy (thermal energies as not yet having been accelerated by the anode).
The Poisson solver can also be useful for other situations in which a charge density distribution is known a priori, such as in the case of a charged insulator material with known charge distribution. This is simpler to handle because it does not require particle flying to do the Refine.
Other applications of the Poisson solver include
Dielectric materials, with known dielectric constants. See Dielectrics.
Solving magnetic vector potential (and hence magnetic fields) from arbitrary distributions of current density in space. See Magnetic Potential.
Solving current density from arbitrary distributions of material conductivity in space and boundary conditions on electric potential. See Current Density.
Floating conductors. See Floating Conductor
Version Requirements¶
Compatibility Warning: The Poisson solving capability is available in SIMION 8.1.0. It is not in previous release versions. The Poisson solving capability is one of the major new features in 8.1.0.
Previous versions of SIMION (8.0 and below) assumed that space-charge density was negligible. That is, it solved only the Laplace equation. However, 7.0 and 8.0 do have some rough “charge repulsion” methods that are useful in approximating space-charge effects under certain conditions (see the SIMION Example: repulsion in SIMION 8.0.4 or above for full details on this). Unlike the SIMION 7.0 Charge Repulsion methods, the Poisson solver takes into account the effect of space-charge on the distribution on surface charges on electrodes (important when high space-charge density is near electrode surfaces).
Math¶
The Poisson Equation is formally

or in the presence of dielectrics,

where  is electrostatic potential as a function of
position
is electrostatic potential as a function of
position  ,
,  is space-charge density as a
function of position,
is space-charge density as a
function of position,  is the relative dielectric constant
as a function of position, and
is the relative dielectric constant
as a function of position, and  is the permittivity of free
space constant. To solve for the potentials (
is the permittivity of free
space constant. To solve for the potentials (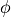 ) inside some
volume, which is done by the Refine function, SIMION must in general know not only
) inside some
volume, which is done by the Refine function, SIMION must in general know not only
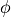 on the boundary of the volume but also
on the boundary of the volume but also 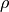 and
and  throughout the inside of that volume.
In the case of no space charge (
throughout the inside of that volume.
In the case of no space charge ( ) and dielectric constant
of 1 outside electrodes (
) and dielectric constant
of 1 outside electrodes ( as is the case of vacuum and approximately
in air), the equation reduces to
the Laplace Equation, which earlier versions of SIMION solved.
as is the case of vacuum and approximately
in air), the equation reduces to
the Laplace Equation, which earlier versions of SIMION solved.
Note
This page is abridged from the full SIMION "Supplemental Documentation" (Help file). The following additional sections can be found in the full version of this page accessible via the "Help > Supplemental Documentation" menu in SIMION 8.1.1 or above:SIMION Array Modeling
Effect of Scaling After Refining
Calculation Method
Usage
Comments on Fast Adjust (.PA#) Files
Comments on magnetic arrays (experimental)
Computing charge density from trajectories
Charge density smoothing
Performance¶
The performance of the Poisson solver will naturally likely be slower than the regular Laplace solver, though not substantially so. The charge density array also uses addition memory. The Pierce gun examples with a non-continuous beam have run times on the order of a few minutes. Using a lower resolution charge density array might speed things up, or at least use less memory.
Thermionic Cathodes¶
For a resistively heated thermionic cathode, the current applied through the heater element raises its temperature and the current that emits from the cathode. Those are two different things, but the latter (emission current) is what we need for the simulation. The emission current is roughly defined by either equation [1] or [2] depending if the temperature is high enough to causes the emission current to be saturated by space-charge.
The distance d in Child’s law assumes a planar diode of infinite radius. In practice, d is a bit arbitrary and typically some point in the local vicinity of the cathode with d small enough that the system looks approximately like a planar diode of infinite radius (relative to length d).
[1] Child’s Law (space-charge limited)
[2] Richardson-Dushman Equation (temperature limited)
Examples¶
See the SIMION Example: poisson for examples on using the Poisson solver. Note that the Poisson solver is an advanced feature. It currently requires Lua user programming to effectively make use of it, but it can be very powerful and flexible. It is recommended that you study the source code.
Also, the Gauss’s Law example may be useful when experimenting with the Poisson solver.
Problems¶
invalid numbers in PA
Be careful when writing to PA’s that you don’t store infinite (1/0 or -1/0) or indeterminate (0/0) values in PA. The following code can check for such values in a PA:
local pa = simion.pas[1]
local vmin = math.huge
local vmax = -math.huge
local x1,y1,z1
local x2,y2,z2
for x,y,z in pa:points() do
local v = pa:point(x,y,z)
if v < vmin then vmin,x1,y1,z1 = v, x,y,z end
if v > vmax then vmax,x2,y2,z2 = v, x,y,z end
if v ~= v or v == math.huge or v == -math.huge then
print("bad point", x,y,z, v)
end
end
print("vmin=", vmin, "x,y,z=", )
print("vmax=", vmax, "x,y,z=", )
Note: -1.#IND (indeterminate) means some indeterminate value (e.g. the result of 0/0) is stored in a point in the PA. What this typically means is that the Lua code wrote some bad value into some point in the PA. Then when you refine, the refine fails because of that bad point. With the Poisson solver, this might be a bad point in the electrostatic PA or the space charge PA, although probably the latter because that is what piclib.lua writes to.
Current Limitations / Caveats¶
The Poisson solver is currently not accessible via the GUI but rather via the Lua programming API.
History/changes¶
8.1.2.20 2014-07-21 - Allow charge weighting factor (CWF) to be negative in particle definitions–useful for Poisson solver piclib.lua.
See Also¶
Child’s Law (space-charge limited)
Richardson-Dushman Equation (temperature limited)