Dielectrics¶
In dielectric materials (i.e. insulators), unlike conductive materials, charges in the molecules or atoms cannot freely move but will shift slightly upon application of an electric field, thereby causing the molecules to become polarized. The cumulative effect of the dipole moments of these polarized molecules or atoms alters the electric field.
Theory¶
The following is a brief summary of the equations and definitions pertaining to electric fields in the presence of dielectrics. For more details and general background, see standard texts like Griffiths and Wikipedia: Dielectric.
Gauss’s Law in differential form, which is one of the
Maxwell Equations and readily derives the
Poisson Equation, is 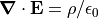 .
In the presence of insulative materials (dielectrics), the charge density
.
In the presence of insulative materials (dielectrics), the charge density
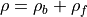 is a sum of bound charge
(
is a sum of bound charge
(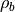 ) from the polarization of the dielectric
and free charge (
) from the polarization of the dielectric
and free charge (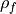 ) from other sources (e.g. electrode surface
charges and space-charge). Since
) from other sources (e.g. electrode surface
charges and space-charge). Since 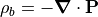 (where P is the polarization, i.e. the dipole moment per unit volume, of
the dielectric), Gauss’
law may alternately be written in terms of free charge as
(where P is the polarization, i.e. the dipole moment per unit volume, of
the dielectric), Gauss’
law may alternately be written in terms of free charge as
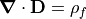 , where we define
, where we define
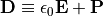 as the electric displacement.
The advantage is that
as the electric displacement.
The advantage is that 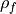 is more likely known than
is more likely known than 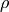 ,
so we can use the Poisson Solver in SIMION to solve for
,
so we can use the Poisson Solver in SIMION to solve for 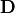 given
given
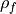 . In some cases
we can then derive E from D.
. In some cases
we can then derive E from D.
In a linear dielectric, 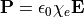 ,
where
,
where 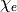 is the electric susceptibility (and is dimensionless). We may
alternately express
is the electric susceptibility (and is dimensionless). We may
alternately express
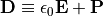 as
as
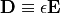 ,
where
,
where 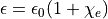 is permittivity,
and
is permittivity,
and 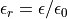 is the relative permittivity,
also called the (relative) dielectric constant. In a non-linear dielectric (but still
isotropic),
is the relative permittivity,
also called the (relative) dielectric constant. In a non-linear dielectric (but still
isotropic), 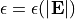 is a function of the
magnitude of the local electric field. In an anisotropic dielectric,
P and E are not necessarily parallel,
is a function of the
magnitude of the local electric field. In an anisotropic dielectric,
P and E are not necessarily parallel, 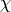 and
and  are tensors rather than scalars.
are tensors rather than scalars.
Putting this together and using 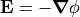 , we have
for a linear dielectric,
, we have
for a linear dielectric, 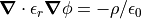 ,
which is a form of the Poisson Equation, which SIMION can solve via the
Poisson Solver in SIMION. This may be solved iteratively, in a self-consistent manner,
in the case of a non-linear, isotropic dielectric.
,
which is a form of the Poisson Equation, which SIMION can solve via the
Poisson Solver in SIMION. This may be solved iteratively, in a self-consistent manner,
in the case of a non-linear, isotropic dielectric.
SIMION Specific - Scope¶
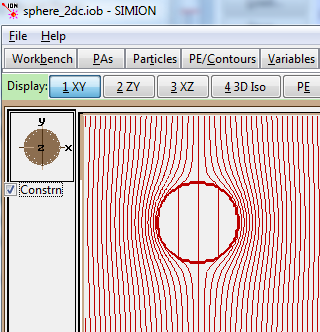
Fig. 57 One of the SIMION 8.1.1 dielectric examples (dielectric sphere inside electric field), with equipotential contour lines shown.¶
SIMION 8.1.1.0 can calculate electric fields in the presence of dielectrics (via the Poisson Solver in SIMION Refine function). It supports linear anisotropic dielectrics, where the relative dielectric constant varies as a function of position. An example is also provided of the more challenging problem of handling non-linear isotropic dielectrics via an iterative (self-consistent) approach. Anistropic dielectrics are not currently implemented. The field solving can incorporate both dielectrics and space-charge effects at the same positions (e.g. a charged dielectric), and anistropically scaled grid cells (not to be confused with anisotropic dielectrics) are supported with dielectrics.
The related problem of solving current densities in the presence of materials of varying conductivity is also supported (see Current Density).
In some cases, the dielectrics are far enough removed from your electrode surfaces that they have little effect on electric fields in the region where particles fly, so you can ignore the dielctrics in the simulation, such as by treating them as non-electrode points. For example, SIMION Example: einzel, there would actually be insulative spacers between the cylinder electrodes, but we ignore those in the model.
SIMION does not presently handle RF effects in dielectrics, where the the dielectric polarization does not instantly respond to changes in electric field but has a frequency dependent response. Those affects are ignored when an RF field in SIMION.
Note
This page is abridged from the full SIMION "Supplemental Documentation" (Help file). The following additional sections can be found in the full version of this page accessible via the "Help > Supplemental Documentation" menu in SIMION 8.1.1 or above:Modeling
Fast Adjust PA# files
Types of dielectrics: Non-linear dielectrics
Types of dielectrics: Isotropic v.s. anisotropic dielectrics
With space-charge
Dielectric charging by a beam (and avoidance of)
Obtaining highest field accuracy on dielectric boundaries
See Also¶
Engineering with non-linear dielectrics X. Qi, Z. Zheng, S. Boggs. DEIS. Nov/Dec 2004 - Vol. 20, No. 6. 27-34.
