Gauss’s Law

Gauss’s Law relates electric flux (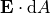\vec{E} \cdot \textrm{d}A) on a surface (S) to the enclosed charge (Q):

\oint_S \vec{E} \cdot \textrm{d}A = \frac{Q}{\epsilon_0} \textrm{, or in differential form: } \bnabla \cdot \vec{E} = \frac{\rho}{\epsilon_0}

See also Wikipedia: Gauss’s_law.

Gauss’s law is closely related to the Poisson Equation (and Laplace Equation), used by SIMION Refine. Gauss’s law is also sometimes useful for Charge-Capacitance Calculation.

Gauss’s Law for Magnetism

Related formulas exists for magnetic fields, but the right-hand-side is always zero assuming magnetic monopoles don’t exist:

\oint_S \vec{B} \cdot \textrm{d}A = 0 \textrm{, or in differential form: } \bnabla \cdot \vec{B} = 0

See also Wikipedia: Gauss%27s_law_for_magnetism.

See Also