Dirichlet Boundary Conditions¶
In solving partial differential equations, such as the Laplace Equation
or Poisson Equation where we seek to find the value of
potential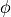 
throughout some volume of space (using methods like SIMION Refine),
it can be necessary to impose constraints on that variable ()
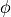at the boundary surface of that space in order to obtain a unique solution
(see First Uniqueness Theorem).
The two main types of these boundary conditions are
Neumann Boundary Condition and Dirichlet boundary conditions.
A Dirichlet boundary condition in the Laplace equation imposes the restriction that the potential is some value at some location. A common case of Dirichlet boundary conditions are surfaces of perfectly conductive electrodes. Free charges in such a conductor will rearrange themselves over the conductive surfaces so that the potential will be uniform over the entire conductor. Typically, electrodes are held to some known potential by attaching them to a power supply or ground, so the Dirichlet condition is known directly, but conductive surfaces may alternately be floating.