Neumann Boundary Condition¶
In solving partial differential equations, such as the Laplace Equation
or Poisson Equation where we seek to find the value of
potential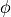 
throughout some volume of space (using methods like SIMION Refine),
it can be necessary to impose constraints on the unknown variable ()
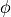at the boundary surface of that space in order to obtain a unique solution
(see First Uniqueness Theorem).
The two main types of these boundary conditions are Neumann boundary conditions
and Dirichlet Boundary Conditions.
A Neumann boundary condition in the Laplace or Poisson equation imposes the constraint that
the directional derivative
of 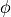is some value at some location.
The typical Neumann boundary condition used is that the directional derivative normal
to some boundary surface, termed the
normal derivative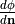 
, is zero.
There are a number of occasions where zero Neumann boundary conditions can occur in a system.
Zero Neumann boundary conditions commonly occur over a plane of mirror symmetry,
which is to say that the potentials at all pairs of points mirrored across a plane
are identical.
For example, an x=0 mirror plane implies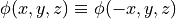 
for all points
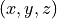in space.
Mirror symmetry in potentials results from mirror symmetry in charge distribution throughout
space (see Coulomb’s Law), which in turn often results from mirror symmetry in electrode
geometry (assuming additional Space Charge doesn’t break that charge symmetry).
Mirror planes exist in many systems (including multipoles like SIMION Example: quad and SIMION Example: octupole).
The zero Neumann boundary condition,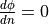 
, exists
at all points on a mirror plane where this derivative 
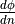exists
(as can be seen by differentiating both sides of ).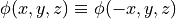
This derivative always exists in empty space (by definition, solutions to the Poisson equation
have second derivatives within the volume).
The derivative might not exist on points on the mirror plane that also happen to have
Dirichlet boundary conditions because there the potential gradient (negative field)
may be discontinuous.
For example, an infinitely thin conductive plate (ideal grid of electrode points in SIMION)
coincident with the mirror plane can cause a field discontinuity.
In 2D cylindrically (axially) symmetric systems, the axis of rotation has infinitely
many mirror planes coincident with the axis, so
the cylindrical axis is also a Neumann boundary condition.
Neumann boundary conditions can also
occur if you have some repeating element such as modeling a small section of a large
grid wire mesh, in which case all sides (left, right, top, and bottom) of
that element might have a Neumann boundary condition.
If a 2D cylindrical array is used to represent a field with no radial component,
such as a uniform field in the axial direction,
a Neumann boundary condition exists on the top Y edge (i.e. lateral cylinder boundary).
Sometimes we also impose Neumann boundary conditions to approximate the far field region:
at some sufficient distance away from some electrodes and their fringe fields,
the field slowly gets close to zero,
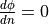which is approximated by even though this derivative is
actually slightly non-zero (e.g. as seen in
SIMION Example: magnet (mag90) or the gaps between electrodes in SIMION Example: einzel).
Neumann boundaries can also be useful if a field has approximately 2D symmetry along the direction perpendicular to the boundary. For example, the Einzel lens in SIMION Example: einzel approximates the condition of the first and third cylinders being infinitely long. To do this, Neumann boundary conditions are specified at approximately field-free regions of the end cylinders, which occur at sufficient distance into the end cylinders. In this case, though, the boundary points are approximately field-free and have known constant potential, so a Dirichlet condition may alternately be used here. A better example is SIMION Example: quad, where the rods are cut with a Neumann boundary plane at a location sufficiently deep into the rods so that the field in the axial direction is zero. Here, traverse components to the fields still do exist, so a Dirichlet condition would not be as easy to specify. This cutting allows the central rod region (quad.pa#) to be solved separately from and at higher accuracy than the quadin.pa# region. In SIMION Example: einzel, Neumann boundary conditions are also used outside the gaps between cylindrical electrodes. This roughly approximates the condition of the tubes being surrounded by empty space. In this case, the gaps are very small, so the fields outside the lens can’t significantly leak into the lens, and even if they do they are relatively small in magnitude compared to the transverse field due to the potential difference between lens elements. That is, the boundary conditions outside the lens are not that important, and to the extent that they do have an effect, a Neumann condition may be more representative of infinite surrounding empty space than a Dirichlet condition. If you do care about fringe effects near open PA boundaries, it is better to add much more empty space near that boundary as shown in the sector magnet example (“examples90.pa#”) so that the fields can more properly expand into that empty space. See First Uniqueness Theorem for more extensive discussion about some of this.
SIMION treatment: In SIMION, non-electrode points on PA edges are always treated as zero Neumann boundary conditions, regardless if mirroring if defined. (Technicality: Prior to 8.1.0, PA edges without a mirror plane defined had boundary conditions very slightly different than Neumann applied, but for practical purposes it could still be considered Neumann – see below.) Examples with interesting Neumann boundaries include SIMION Example: octupole (multipole), SIMION Example: einzel (2D cylindrical + fringe fields), SIMION Example: nonideal_grid (repetition), and SIMION Example: magnet (mag90, having fringe fields).
Differences between SIMION 8.0 and 8.1¶
Previously, in SIMION 8.0, Neumann boundary conditions were only defined explicitly for edges with a mirror plane defined, and mirror planes can only be defined as X=0, Y=0, and Z=0 planes (and are imposed as Y=0 for 2D cylindrical arrays). All other edges had a condition applied that was less rigorously defined though effectively very close to, but slightly different from, the Neumann boundary condition. This difference decreased to zero as the grid density approached infinity, so in practice it could usually be used as a Neumann boundary condition. In SIMION 8.1, we do away with this latter type of boundary condition because it has no known advantage but does have some minor disadvantages.
Note
This page is abridged from the full SIMION "Supplemental Documentation" (Help file). The following additional sections can be found in the full version of this page accessible via the "Help > Supplemental Documentation" menu in SIMION 8.1.1 or above:Differences between SIMION 8.0 and 8.1 - Calculation Methods
Field interpolation - Calculation Methods