Hemispherical Deflection Analyzer (HDA)¶
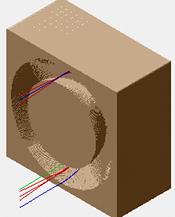
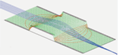
Fig. 42 Idealized HDA showing electrons with energies 1000 eV (red), 900 eV (green), and 1100 eV (blue).¶
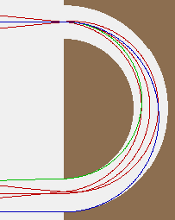
Fig. 43 2D cross-section of previous figure.¶
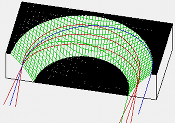
Fig. 44 Potential energy (PE) view of previous figure.¶
The Hemispherical Deflection Analyzer (HDA) consists of two concentric hemispherical electrodes held at different potentials. Charged particles of only a certain kinetic energy (KE), called the pass energy, can pass through the electrodes, and particles at energies sufficiently lower or higher will hit the walls or apertures, so the system acts as a narrow band KE filter.
A picture of a SIMION simulation of an HDA is shown in Figures 1-3. This HDA allows through electrons with energies between roughly 900 and 1100 eV. The HDA also has a focusing effect: 1000 eV electrons (red) focused at the top entrance regain focus at the bottom entrance.
A real HDA has fringe fields at the entrance and exit,
which may or may not be corrected, but for
easier understanding we may approximate it without fringe fields.
This idealized HDA has the electric field of the
so-called spherical capacitor, consisting of two concentric
spherical electrodes held at different potentials. The spherical
capacitor has simple analytic formulas for potential 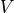 and electric field
and electric field 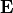 at radius
at radius  :
:
(1)¶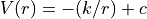
(2)¶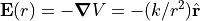
where
(3)¶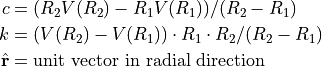
The pass energy 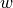 at
at 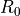 is
is
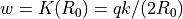 , for particle charge
, for particle charge
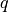 .
.
The above equations are not exactly valid at higher velocities when relativistic effects occur. (As a test, you might try How do I disable relativistic effects? to temporarily disable relativitic effects in order to gauge the signficiance of relativistic effects.)
Modeling¶
Typical GEM files for sperical capacitors are given
below. Here, 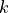 = -200000,
= -200000,  = -2000,
= -2000,
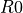 = 100,
= 100, 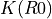 = 1000 eV, and
= 1000 eV, and 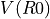 = 0. The inner and outer radii are
= 0. The inner and outer radii are 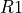 = 80 mm and
= 80 mm and
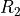 = 120 mm.
= 120 mm.
Here is a typical 2D GEM file (using “fractional” surface enhancement for highest accuracy, under SIMION >= 8.1.1):
; sc2d.gem
pa_define(130,130,1,cylindrical,xy, surface=fractional)
; outer electrode, R2
e(-333.3333) { fill { notin { circle(0,0,120) } } }
; inner electrode, R1
e( 500.0000) { fill { within { circle(0,0,80) } } }
Optionally surface=fractional may be replaced with
surface=auto in >= 8.1.1.25, but that is less accurate
(see surface=auto option in pa_define [8.1.1.25]).
Here is typical code for previous SIMION versions.
Note the notin_inside
(but see the surface=auto discussion for improving accuracy further):
; sc2d.gem
pa_define(130,130,1,cylindrical,xy)
; outer electrode, R2
e(-333.3333) { fill { notin_inside { circle(0,0,120) } } }
; inner electrode, R1
e( 500.0000) { fill { within { circle(0,0,80) } } }
Here is a typical 3D GEM file (using “fractional” surface enhancement for highest accuracy, under SIMION >= 8.1.1):
; sc3d.gem
pa_define(130,130,130,planar,xyz,surface=fractional)
; outer electrode, R2
e(-333.3333) { fill { notin { sphere(0,0,0,120) } } }
; inner electrode, R1
e( 500.0000) { fill { within { sphere(0,0,0,80) } } }
If creating a PA# file, you may replace the two voltages with 1 and 2 to permit fast adjusting.
The 3D GEM file consumes a lot more RAM than the 2D version, but if you need to add any feature to this geometry that breaks the 2D symmetry (e.g. entrance/exit slits), you likely will need the 3D form.
If you omit the “x” mirroring in the pa_define statement, then
an idealized HDA will be represented (i.e. just one half of the sphere).
The boundary condition for potentials on the x=0 plane is assumed by SIMION to
be approximately a Neumann condition (derivative of potential along
normal to the x=0 plane equal to zero), which is the same
condition that exists in the spherical capacitor. In theory, an idealized
HDA could be constructed by covering the X=0 plane with an ideal (100% transmission)
grid that has a variable potential over its surface exactly matching Equation
(1).
In practice, such a grid can only be approximated (e.g. with a series of thin
wires), and some fringing fields will always exist near this X=0 plane.
To model a real HDA with fringe fields, you would include in your potential array the space and electrodes surrounding the entrace/exit (like in the SIMION Example: hda – Figure 4).
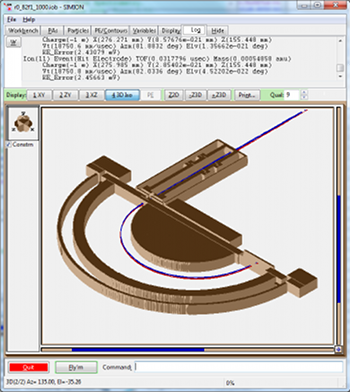
Fig. 45 SIMION “hda” example (Zouros), run at higher mesh resolution and displayed with cross section cut-out.¶
See Electrode Surface Enhancement / Fractional Grid Units for a way to improve electric field calculation accuracy by more than an order of magnitude. SIMION Example: surface_enhancement (SIMION 8.1.1.10) demonstrates this for an HDA.
See also¶
T.J.M. Zouros, Omer Sise, F.M. Spiegelhalder, and David J. Manura. “Investigation of the accuracy of ion optics simulations using Kepler orbits in a spherical capacitor.” International Journal of Mass Spectrometry. 2006. doi:10.1016/j.ijms.2006.08.005 Note: the SIMION 8.1.1 Electrode Surface Enhancement / Fractional Grid Units feature (demonstrated for an HDA in SIMION Example: surface_enhancement) greatly improves accuracy beyond the results in this paper.
Surface Analysis Forum: HDA - Hemispherical Deflection Analyser
Zouros, Benis, Schauer, “Charged particle trajectories in an ideal paracentric hemispherical deflection analyser.” AIP Conference Proceedings, Volume 576, Issue 1, pp. 76-79, 2001. doi:10.1063/1.1395253; online
Zouros and Benis. “The hemispherical deflector analyser revisited. I. Motion in the ideal 1/r potential, generalized entry conditions, Kepler orbits and spectrometer basic equation.” Journal of Electron Spectroscopy and Related Phenomena 125 (2002) 221-248. doi:10.1016/S0368-2048(02)00137-8; online; erratum
Zouros and Benis. “Optimal energy resolution of a hemispherical analyzer with virtual entry.” Applied Physics Letters 86, 094105, 2005. doi:10.1063/1.1871339; online
Benis and Zouros. “Improving the energy resolution of a hemispherical spectrograph using a paracentric entry at a non-zero potential.” NIMPRA 440 (2000) 462-465 doi:10.1016/S0168-9002(99)00954-7; online
Sise, Zouros, Ulu and Dogan, 2007, “Novel and traditional fringing field correction schemes for the hemispherical analyser: Comparison of first-order focusing and energy resolution.” Meas. Sci. Tech. 18 1853-1858. doi:10.1088/0957-0233/18/7/009
Dogan, Ulu, and Sise, 2007, “Design of electron energy analysers for electron impact studies.” Rad. Phys. Chem. 76 445-449. doi:10.1016/j.radphyschem.2006.01.017
T.J.M. Zouros. “Theoretical investigation of the energy resolution of an ideal hemispherical deflector analyzer and its dependence on the distance from the focal place.” Journal of Electron Spectroscopy and Related Phenomena 152 (2006) 67-77. doi:10.1016/j.elspec.2006.03.007 (erratum) corrects line shapes)
DoganUlu2013. Dogan, M.; Ulu, M.; Gennarakis, G. G.; Zouros, T. J. M. Experimental energy resolution of a paracentric hemispherical deflector analyzer for different entry positions and bias. Review of Scientific Instruments, volume 84, issue 4, year 2013, pages 043105. doi:10.1063/1.4798592 – energy resolution of a paracentric HDA, evaluated with experiment and simulation (SIMION 8.1.1 surface enhancement with many run parameterizations).
DoukasMadesis2015. Doukas, S.; Madesis, I.; Dimitriou, A.; Laoutaris, A.; Zouros, T. J. M.; Benis, E. P. Determination of the solid angle and response function of a hemispherical spectrograph with injection lens for Auger electrons emitted from long lived projectile states. Review of Scientific Instruments. volume 86, issue 4, year 2015, pages 043111. doi:10.1063/1.4917274 [see also poster] – “In this report, we have shown how a Monte Carlo type approach can be combined with SIMION to accurately simulate a high resolution projectile Auger electron spectrum recorded by a hemispherical spectrograph with injection lens and 2D position sensitive detector.” “…at each point of the ionic trajectory z, a number of emitted electrons is determined proportional to the product of the decay term and the solid angle term in Eq. (19) as illustrated in Fig. 4 and then multiplied by a starting indicative number Ni that determines the total number of electrons to be flown.” Uses SIMION simulations.
SiseZouros2015. Sise, Omer; Zouros, Theo J. M. Position, Energy, and Transit Time Distributions in a Hemispherical Deflector Analyzer with Position Sensitive Detector. Journal of Spectroscopy. volume 2015, year 2015, pages 1-20. doi:10.1155/2015/153513. – “Here, we have explored for the first time the time-offlight properties of the biased paracentric HDA for the two special entry positions already investigated in the past as to their energy resolution and compared them to those of the conventional HDA…” Uses SIMION simulations.
O. Sise, G. Martínez, I. Madesis, A. Laoutaris, A. Dimitriou, M. Fernández-Martín, T.J.M. Zouros. The voltage optimization of a four-element lens used on a hemispherical spectrograph with virtual entry for highest energy resolution. Journal of Electron Spectroscopy and Related Phenomena. Volume 211, August 2016, Pages 19-31. doi:10.1016/j.elspec.2016.05.004. “We investigate the voltage settings for the four-element injection lens of an HDA. The two well-known approaches, BEM and FDM, in charged particle optics were used. We tested optimal lens voltages from simulation on the actual experimental setup. The measured FWHM were well modeled using realistic source parameters.”
BenisMadesis2018. Benis, E.P. Madesis, I. Laoutaris, A. Nanos, S. Zouros, T.J.M. Experimental determination of the effective solid angle of long-lived projectile states in zero-degree Auger projectile spectroscopy. Journal of Electron Spectroscopy and Related Phenomena. volume 222, year 2018, pages 31-39. doi:10.1016/j.elspec.2017.10.001.
J.H. Vilppola, J.T. Keisala, P.J. Tanskanen, and J. Huomo. “Optimization of hemispherical electrostatic analyzer manufacturing with respect to resolution requirements.” Rev. Sci Instrum. 64 (8), August 1993. doi:10.1063/1.1143958
Wannberg1985 B. Wannberg. Effects of mechanical imperfections in a hemispherical electron spectrometer Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. volume 239, issue 2, year 1985, pages 269-272 doi:10.1016/0168-9002(85)90725-9
“Advances in Imaging and Electron Optics: Electron Physics: Optics of Charged Particle, Volume 157” by Mikhail Yavor has a chapter on many types of energy analyzers, including HDA’s, with SIMION screenshots. This chapter is also available at doi:10.1016/S1076-5670(09)01606-1 .
The voltage optimization of a four-element lens used on a hemispherical spectrograph with virtual entry for highest energy resolution O. Sise, G. Martínez, I. Madesis, A. Laoutaris, A. Dimitriou, M. Fernández-Martín, T.J.M. Zouros. – four-element lens optimization with hemispherical deflector analyzer (HDA) and PSD detector, with SIMION FDM as well as BEM following by experimental confirmation.
http://www.sciencedirect.com/science/article/pii/S1076567009016061