Magnetic Sector

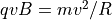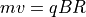A charged particle (mass m and charge q) with velocity v perpendicular to a uniform magnetic field B will (by the Lorentz Force Law) experience a centripetal force , sustaining a circular motion of radius R in the plane perpendicular to the magnetic field [4] [3] . This equation is called the cyclotron formula [1] [2], and it may be rewritten as , thereby showing that the gyroradius [2], R, is proportional to momentum, if charge is constant. A uniform magnetic field therefore can act as a momentum analyzer (in contrast to electric fields used in kinetic energy analyzers like in the Hemispherical Deflection Analyzer (HDA)).

A magnetic sector is a type of mass analyzer using a static magnetic field to deflect particles in this way along a roughly circular arc. It is characterized by a deflection angle 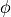and radius 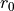. For background/theory, particularly on focusing properties in design, see [5] [6] [7].

See also Hemispherical Deflection Analyzer (HDA), which is combined with a magnetic sector in a double focusing magnetic sector.

SIMION specific

See SIMION Example: magnet (mag90.iob) for a simple 3D simulation with cylindrical poles and fringing fields. SIMION Example: magnetic_sector (added in 8.1.1.0) is a more extensive example, which examines focusing properties of various magnetic sector geometries (inclined and conical, 2D and 3D) with full control of parameters. The HIPIRMS course [8] includes other SIMION magnetic sector models and discussions. The Short ASMS Course (courses\short) (Session 2) has a brief look at sectors. SIMION simulations of sectors are illustrated in the discussions in [6]. Magnetic poles with approximately infinite permeability and treated with scalar magnetic potential are the easiest to handle (see Magnetic Potential).

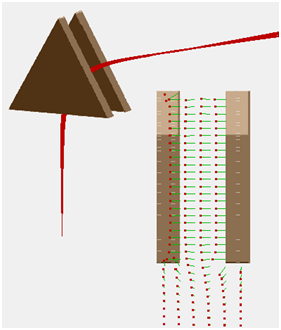
Fig. 45 Figure: SIMION Example: magnetic_sector - 60 degree 3D sector (with fringe fields) and B-field vectors.

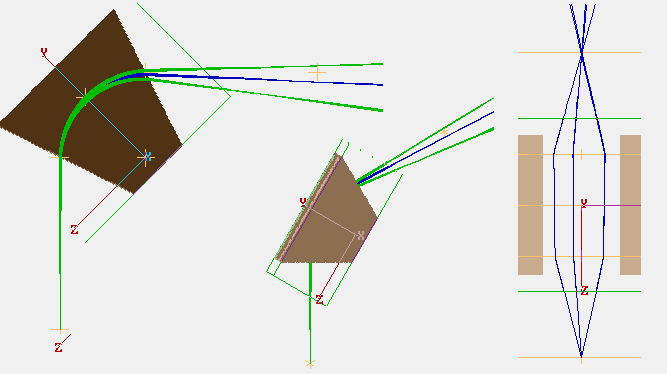
Fig. 46 Figure: SIMION Example: magnetic_sector - 90 degree 3D sector (with fringe fields) and inclined 26.56 degree entrance/exit angles to achieve symmetric stigmatic focusing.

References

[1]

http://scienceworld.wolfram.com/physics/Cyclotron.html

[2] (1,2)

Wikipedia: Gyroradius

[3]

SIMION 8.1 printed manual. Section 2.2 “Basic Ion Optics Concepts”.

[4]

David Jeffery Griffiths. Introduction to electrodynamics. G: M8XvAAAAMAAJ. 1999. Prentice Hall. ISBN: 978-0-13-805326-0. Section 5.1 “The Lorentz Force Law”.

[5]

Helmut Liebl. Applied charged particle optics. November 2007. Springer. G: XqRFZX0ssRMC ISBN: 978-3-540-71924-3 springer. Chapter 3. Magnetic Deflection.

[6] (1,2)

Mikhail Yavor. Advances in Imaging and Electron Physics: Optics of Charged Particle Analyzers. Volume 157 of Advances in Imaging and Electron Physics. G: ntYf2V-pbIgC. 24 July 2009. Academic Press. ISBN: 978-0-12-374768-6. Chapter 5. Static Magnetic Charged Particle Analyzers.

[7]

Jürgen H. Gross. Mass Spectrometry: A Textbook. G: xHOQiaquq24C. 6 April 2011. springer. ISBN: 978-3-642-10709-2. Section 4.3. Magnetic Sector Instruments. See also http://www.ms-textbook.com/.

[8]

HIPIRMS http://hipirms.org/ has SIMION course notes and examples related to magnetic sectors. Topic 3 and Session 3 are on magnetic sectors. d3_lecture.ppt - summary on magnetic sector theory.

[9]

Wikipedia: Sector_instrument