Transfer Matrix¶
The propagation of paraxial rays through a series of lenses can be conveniently approximated by a matrix approach.
To take a simple case, assume that each particle in a 2D cylindrically
symmetric lens system can be uniquely described at an axial position z
by a vector 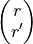 , where r is the
radial distance of the particle from the axis and r’ is the
slope of the ray (
, where r is the
radial distance of the particle from the axis and r’ is the
slope of the ray (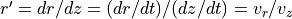 , for time t and velocity v).
The states of the particle
, for time t and velocity v).
The states of the particle
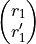 and
and
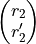 respectively at planes
respectively at planes 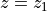 and
and 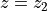 near the entrance and exit of a lens respectively
can be related by a matrix equation:
near the entrance and exit of a lens respectively
can be related by a matrix equation:
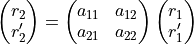
where the matrix ![\v{A} = \left[ a_{ij} \right]_{2x2}](_images/math/db58bacbf9c8dca796fc287107d15f9e0dca26ce.png) is referred to as the transfer matrix and is specific to the
plane locations and lens. The matrix coefficients can depend on parameters
such as focal lengths. If you partition your optic axis by a series of
(transverse) planes,
then the transfer matrix between the outermost planes
is the product of all the transfer matrices between successive planes.
is referred to as the transfer matrix and is specific to the
plane locations and lens. The matrix coefficients can depend on parameters
such as focal lengths. If you partition your optic axis by a series of
(transverse) planes,
then the transfer matrix between the outermost planes
is the product of all the transfer matrices between successive planes.
The transfer matrix can have larger dimensions if motion in more than one direction (here, r) and/or aberations are taken into account.
Many books such as those cited below [1] [2] [3] [4] describe the transfer matrix approach in more detail. [1] briefly provides matrix coefficients in terms of cardinal points in 2D cylindrical lens. A more general and detailed treatment is in [2]. [3] makes extensive use of transfer matrices throughout in its derivations. [5] has a description in the context of various components in mass spectrometry. The analogous concept is used in light optics (ray transfer matrix analysis or ABCD matrix analysis–see BYU tutorial). The concept is also related to Hamiltonian mechanics (see also Emittance).
SIMION-specific¶
Transfer matrices are not normally used directly by SIMION because SIMION is equipped to take the more general, more accurate, and more computationally intensive approach of computing the entire trajectory of each particle (position as a function of time) from the fully known (or calculated) electromagnetic field; it does this by integrating the Lorentz Force Law. You may, however, wish to use SIMION to compute the lens properties (and hence transfer matrices) of some arbitrarily shaped lenses (SIMION Example: lens_properties) in the first place.
