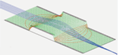
Mathieu Equation and Stability Diagram

The Mathieu differential equation [1] is a differential equation of the form

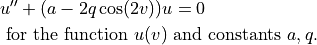
& u'' + (a - 2q \cos(2 v))u = 0 \\ & \textrm{ for the function } u(v) \textrm{ and constants } a, q.

One area, of interest to us, where this occurs is the equation of motion for particles in an ideal quadrupole Ion Trap (see [2-3]), where u is a coordinate in space (e.g. x) and v is proportional to time t. We can see this by relating (via the Lorentz Force Law) the particle acceleration (x’‘) to the equations for the gradient of the quadrupole field potential 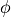\phi:

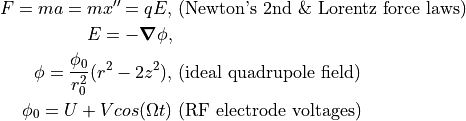
F = m a = m x'' = q E, & \textrm{ (Newton's 2nd \& Lorentz force laws) } \\ E = - \grad \phi, & \\ \phi = \frac{\phi_0}{r_0^2}(r^2 - 2z^2), & \textrm{ (ideal quadrupole field) } \\ \phi_0 = U + V cos(\Omega t) & \textrm { (RF electrode voltages) }

The stability of the particle motion in the trap depends on the constants a and q, which we can see are functions of the trap voltages (U and V), angular frequency (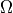\Omega), and particle m/z ratio. [2-3]

Even in ion traps with non-idealized geometries, such as hyperbolic electrodes replaced with circular or flat ones, fields maintain some resemblance to the ideal case, and the formalism of a & q still applies.

A Mathieu stability diagram plots regions of the u-v space that lead to stable trajectories, and they are often depicted in introductions to ion trap theory (e.g. [2-3]).

SIMION specific

SIMION can solve not just the Mathieu equation but the more general problem of determining particle trajectories most any type of Ion Trap (not limited to idealized traps) or other type of system. You can simulate in SIMION various ion traps and observe how choices of a & q lead to stable or unstable particles trajectories. In fact, SIMION Example: quad conveniently sets quadrupole mass filter voltages based on a & q parameters entered. It would be possible to generate a Mathieu stability diagram from SIMION data (ways to automate multiple runs, like in SIMION Example: tune, can help too).